Бинокли
Чтобы стрелять из орудия, надо прежде всего знать, куда стрелять и по какой цели. Раньше, когда стрельба артиллерии велась на небольшие дальности и по хорошо видимым простым глазом целям, орудия наводили при помощи самых простых приборов — целика и мушки. В настоящее время мы также пользуемся целиком и мушкой при стрельбе из винтовки, автомата и пистолета.
В современной же войне, когда артиллерийские орудия, как правило, стреляют с закрытой огневой позиции по невидимым целям, когда приходится непрерывно наблюдать за полем боя и отыскивать цели, находящиеся на большом удалении, используются разнообразные артиллерийские приборы, среди которых наиболее важное место занимают оптические приборы.
В условиях современной войны даже в снайперской винтовке используются не только обычные целик и мушка, но и оптический прицел, артиллерийские же орудия являются наиболее сложными машинами, поэтому для стрельбы из них необходимы специальные прицельные приспособления и различные приборы.
Ниже приводится описание наиболее употребительных артиллерийских приборов, которыми являются: бинокль, перископ, стереотруба, буссоль.
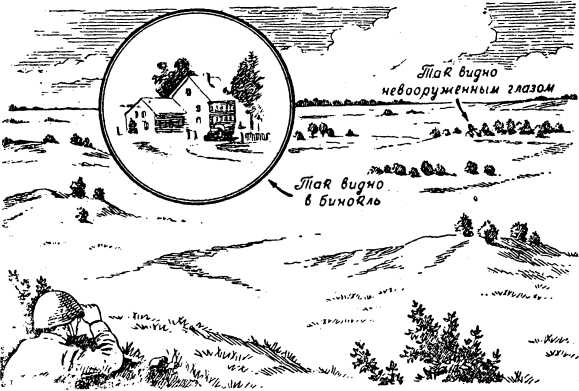
Бинокль — наиболее распространенный наблюдательный и углоизмерительный оптический прибор. Прибор этот дает возможность тщательно рассматривать местность и расположенные на ней предметы, изображение которых в приборе получается увеличенным и приближенным. Так, например, если мы будем наблюдать местность невооруженным глазом и при помощи бинокля, то заметим значительную разницу в видимости предметов (рис. 49).
Рис. 49. Наблюдение вооруженным и невооруженным глазом.
Бинокли используются для наблюдения за полем боя, для отыскания целей и их изучения, для измерения углов и для корректирования стрельбы.
Устройство бинокля очень простое. Он состоят из двух зрительных труб, соединенных шарнирной осью (рис. 50).
Рис. 50. Призменный бинокль и его сетка.
В каждой зрительной трубе на одном конце имеется вращающаяся окулярная трубка с окуляром, а на другом конце — объектив. Внутри самой трубы помещаются две призмы.
Линзы и призмы в бинокле расположены так, что наблюдающий видит прямое и увеличенное изображение рассматриваемых предметов.
На окулярной трубке зрительной трубы имеется шкала с делениями от нуля до плюс пять в одну сторону и от нуля до минус пять в другую сторону.
На зрительной трубе, в ее верхней части мы видим черточку (риску), против которой устанавливается необходимое деление.
Цифра ноль соответствует нормальному глазу, цифры со знаком минус — близорукому и цифры со знаком плюс — дальнозоркому.
Значит, шкала эта с делениями необходима для того, чтобы подогнать бинокль по глазам. Делается это следующим образом: наблюдая в бинокль, выбирают на местности какой-нибудь предмет с отчетливыми очертаниями, в него наводят одну из труб (при этом другой глаз закрывать не следует). Затем поворачивают окулярную трубку до тех пор, пока не будет получено совершенно четкое изображение. То же надо сделать и с другим окуляром для другого глаза.
На шарнирной оси сверху тоже имеется шкала с делениями. Эти деления необходимы для того, чтобы устанавливать зрительные трубы в соответствии с расстоянием между зрачками, так как это расстояние у различных людей неодинаково.
Подогнав таким образом бинокль по глазам, запоминают деления для левого и правого глаза, а также и деление, указывающее расстояние между глазами; в дальнейшем устанавливают эти деления заблаговременно.
При наблюдении в бинокль мы замечаем, что в поле зрения имеется шкала с делениями в виде черточек и крестиков. Эта шкала с делениями предназначена для измерения углов (см. рис. 50).
В обыденной жизни, как известно, углы измеряются градусами, минутами и секундами. Вся окружность делится на 360 градусов, в градусе 60 минут, а в минуте 60 секунд. Для артиллерийских приборов измерение углов в градусах очень неудобно из-за сложности расчетов, поэтому артиллеристы изобрели особую меру для измерения углов — так называемую тысячную, которая наносится на артиллерийские приборы и соответствует одному маленькому делению угломера.
Такие деления мы видели на кольце угломера и на кольце барабана угломера панорамы, с устройством которой мы уже ознакомились. Окружность, как мы заметили, делится там на 6000 делений. За основную меру для измерения углов в артиллерии и принимают одну шеститысячную долю этой окружности. Попытаемся определить ее величину в долях радиуса. Из геометрии известно, что длина окружности превосходит длину ее радиуса приблизительно в шесть раз. Значит, одна шеститысячная часть окружности будет равна одной тысячной радиуса окружности, т. е. дальности. Поэтому-то эта мера и носит название «тысячной».
Теперь можно сказать, что в поле зрения бинокля мы как раз и видели деления — тысячные. Самое маленькое деление равно 5 тысячным; оно пишется так: 0-05, а произносится ноль-ноль пять. Большое деление равно десяти тысячным и пишется 0-10, а произносится ноль-девять.
Всего маленьких делений 20 (по 10 в каждую сторону от крестика в середине).
Кроме горизонтальных делений, имеется еще четыре деления вертикальных, общей ценой в двадцать тысячных.
Зная, что такое тысячная, попытаемся решить, пользуясь биноклем, некоторые задачи.
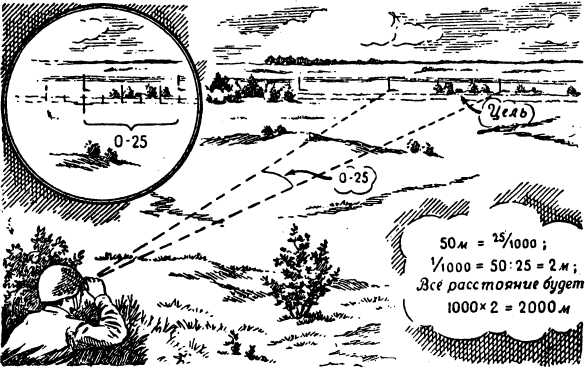
Нам нужно, например, определить расстояние до вражеского пулемета, находящегося у шоссейной дороги. Для решения этой задачи воспользуемся известной нам величиной — расстоянием между телеграфными столбами, которое обычно равно 50 м (рис. 51).
Рис. 51. Определение расстояния до пулемета.
Затем биноклем определяем угол, под которым видно с наблюдательного пункта расстояние между столбами. Угол этот, оказывается, равен 0-25 (25 тысячных). Значит, 25 тысячных равны 50 м, а одна тысячная будет равна 50: 25 — 2 м. Отсюда нетрудно сосчитать и расстояние до пулемета. Над только представить себе, что наблюдательный пункт является центром окружности, радиус которой мы хотим определить. А так как 2 м являются одной тысячной долей этого радиуса, то весь радиус будет равен 2000 м.
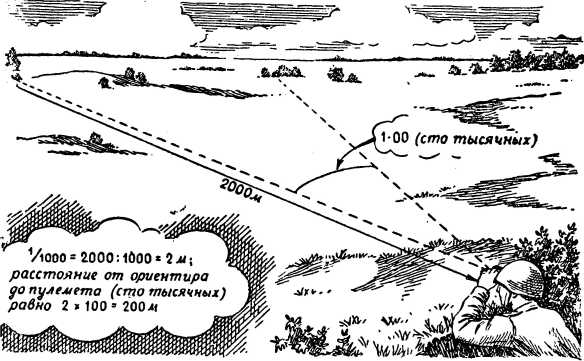
Теперь мы определили угол 1-00 (сто тысячных), под которым виден пулемет противника от нашего ориентира — отдельно стоящего дерева. Мы хотим знать, какое же расстояние от пулемета до дерева. В этом случае нам известно, что расстояние до дерева и до пулемета равно 2000 м. Значит, одна тысячная будет равна 2000: 1000 = 2 м, а сто тысячных будут равны 200 м. Значит, расстояние от дерева до пулемета 200 м (рис. 52).
Рис. 52. Определение расстояния от отдельно стоящего дерева до пулемета.